1. 34.567/56
2. 6.578/ 7
15 de abril de 2020
- 56x300
- 320x200
- 89 x 4000
- 4.500/50
- 8.400/300
Actividad 4: Dibuja tres ángulos en tu cuaderno, grabate midiendolos y di que tipo de ángulo es, cuando lo tengas, envíame el video al whatsApp.
Tarea: Ingresa al siguiente link: https://www.cokitos.com/juego-de-medir-angulos/play/ y realiza la actividad propuesta, una vez termines, tómale un pantallazo a la computadora y enviame tus respuestas.
Observa el siguiente video y aprende cómo jugar
2. Responde las siguientes preguntas en tu cuaderno, si tienes la posibilidad, imprime las imágenes:
Ingresa al siguiente Link y únete a la videoconferencia:
https://meet.google.com/ysh-rjau-yav
Actividad: Realiza las páginas 45, 47 y 49 de exploradores.
Tarea: Realiza las páginas 214, 215 y 216 de exploradores.
6 de mayo del 2020
Ingresa al siguiente link para la videoconferencia:
https://meet.google.com/ghj-yzxp-pri?hs=122&authuser=2
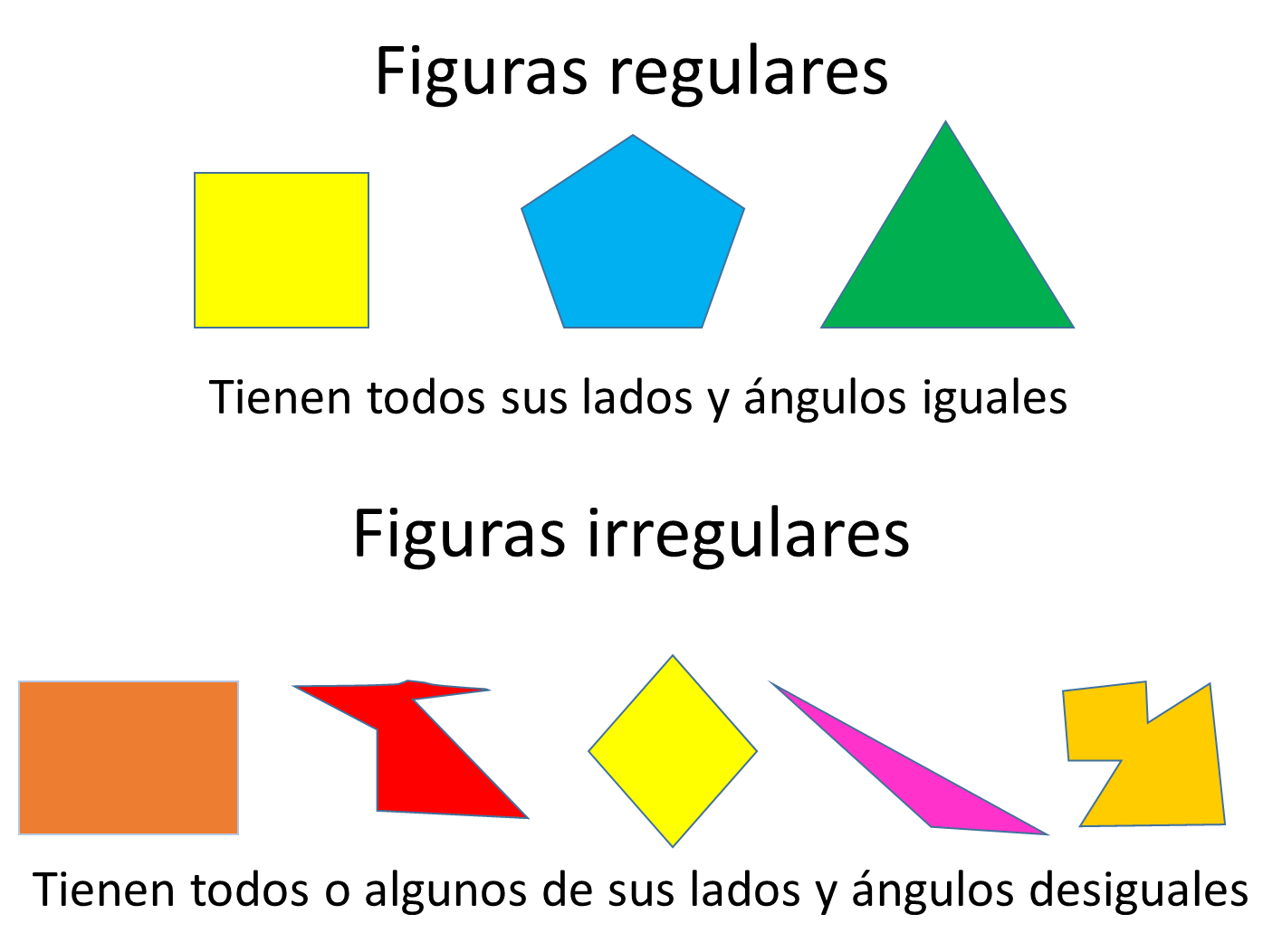
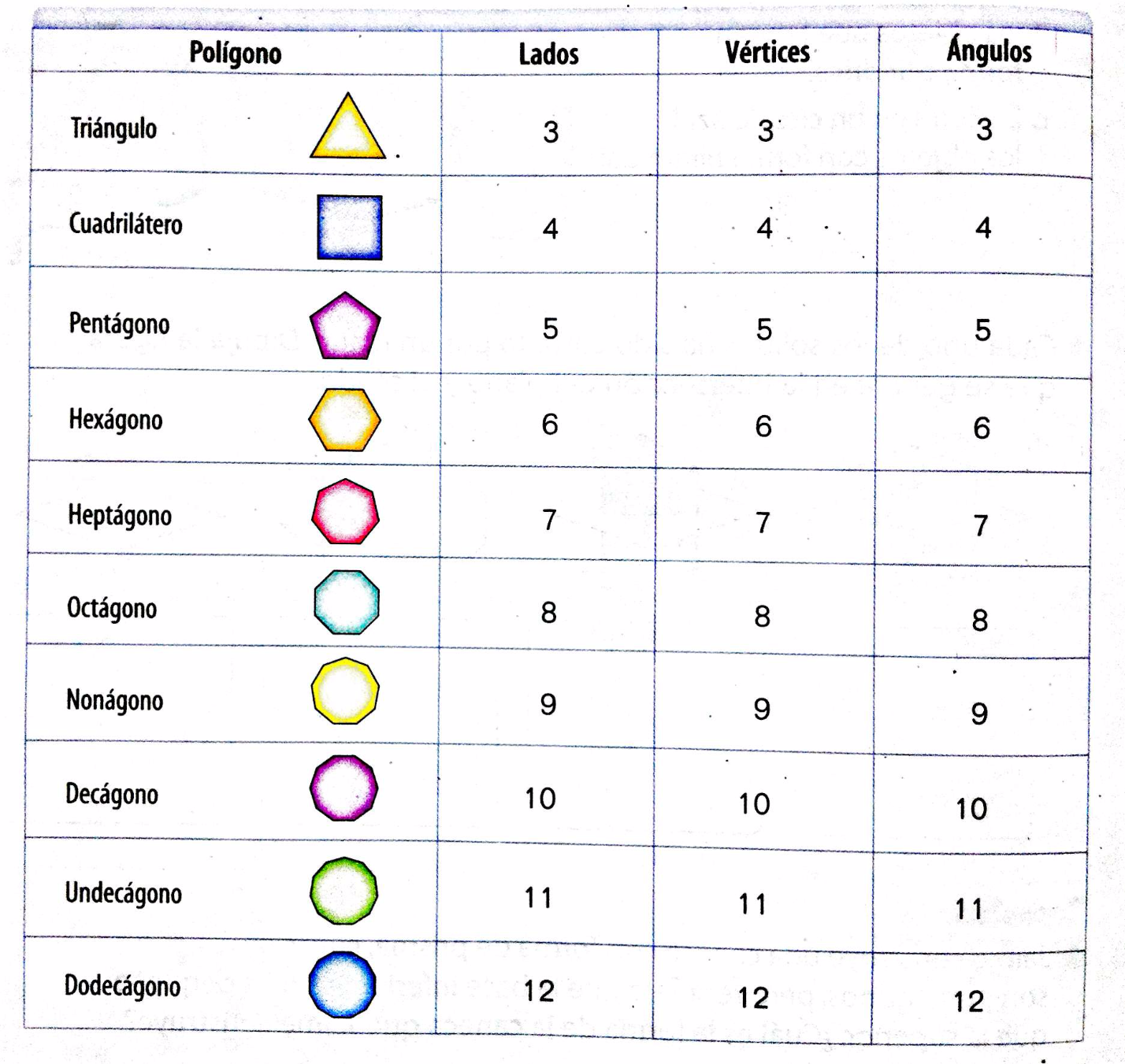
Polígonos regulares e irregulares
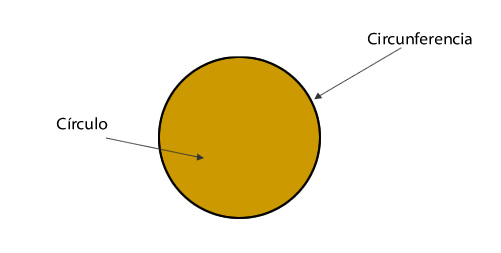
- Centro punto del interior de la circunferencia tal que la distancia desde él a cualquier punto de la circunferencia es la misma.
- Radio es el segmento que une el centro con cualquier punto de la circunferencia.
- Diámetro es el segmento que tiene por extremos dos puntos de la circunferencia y que pasa por el centro. El diámetro es el doble del radio. D = 2·R
- Cuerda es el segmento que une dos puntos cuales quiera de la circunferencia. La cuerda mayor de una circunferencia es el diámetro.
- Arco parte de la circunferencia comprendida entre dos puntos.
- Semicircunferencia es cada una de las partes en que un diámetro divide a una circunferencia, es decir, media circunferencia.
¡Practiquemos!
El radio y el diámetro
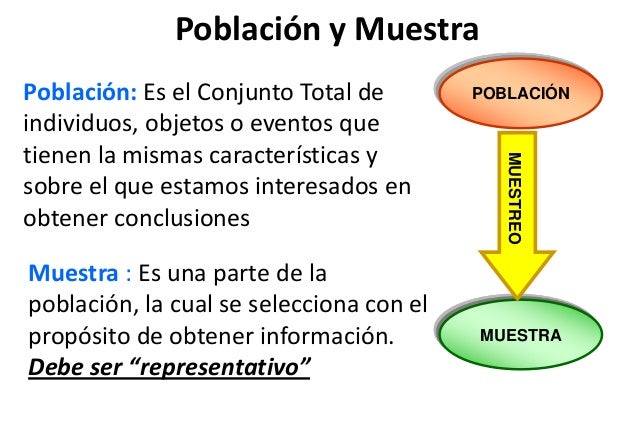
La estadística
Conjunto de métodos científicos ligados a la toma, organización, recopilación, presentación y análisis de datos, tanto para la deducción de conclusiones como para tomar decisiones razonables de acuerdo con tales análisis.
Elementos de la estadística:
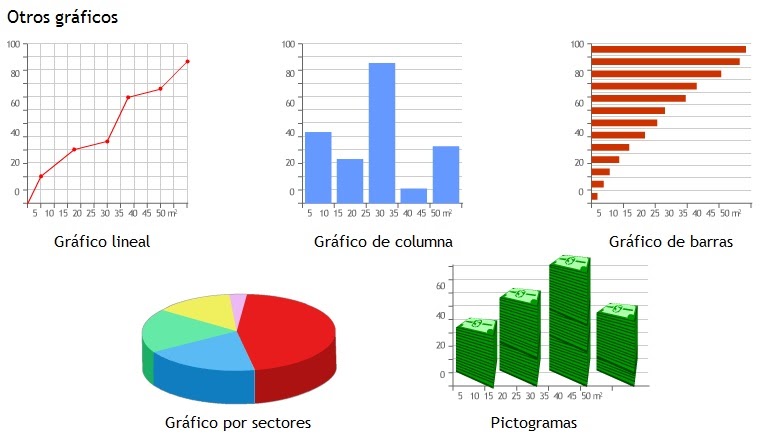
¿Cómo se organizan los datos? Las tablas de datos: Una tabla de datos es una colección de datos organizados en filas y columnas.
- Primero sumo todas las cantidades anteriores: 9 +10 + 4 + 6 + 9 + 6 + 8 + 9 + 1 + 9 + 6 + 9 + 4 = 90
- El resultado de la suma se divide entre el total de los números sumados: 90 ÷ 13 = 6.9
- M=6.9
- Primero hay que ordenarlos de menor a mayor: 1, 4, 4, 6, 6, 6, 8, ,9, 9, 9, 9, 9, 10.
- Se cuentan los datos, en este caso son trece valores, el trece es impar.
- Ahora, se debe localizar el que se encuentra en el centro.
- Quedan seis datos antes del centro y seis después. 1, 4, 4, 6, 6, 6, 8, 9, 9, 9, 9, 9, 10
- La mediana de este conjunto es 8. Md = 8
- Ordeno de mayor a menor y busco los dos que quedan al centro de la serie 1, 4, 4, 6, 6, 6, 8, 9, 9, 9, 9, 9, 10,6.
- Ahora saco el promedio de 8 y 9
- 8 + 9 = 17 ÷ 2 = 8.5
- La mediana es 8.5 Md = 8.5
- Dados los datos (5,3,5,5,4,2,5,7,8,9,9,6,5) halla:
- La mediana=
- La moda=
- la media=
- El rango=
- La mediana=
- La moda=
- la media=
- El rango=
Miércoles 27 de mayo de 2020
Medidas de tendencia central
Múltiplos y divisores
https://meet.google.com/rtd-qvng-kdg?hs=122&authuser=2
Realiza las páginas 78 y 79 de exploradores.
Tarea: Realiza las páginas 226 y 227 de exploradores.
- Se escribe el número a la izquierda de una raya vertical (actúa como "ventana" de división) y a su derecha el menor número primo (2, 3, 5, 7,... ) por el cual dicho número sea divisible. El cociente obtenido se coloca debajo del número propuesto.
- Se procede como en el paso anterior con el cociente obtenido, y así sucesivamente hasta llegar a un cociente igual a 1.
- Realiza la descomposición en factores primos de los siguientes números: 1250, 480, 210.
- Realiza el punto 2 y 3 de la página 85 de exploradores.
https://meet.google.com/xse-zjcb-vca?hs=122&authuser=2
Actividad #1
- Realiza el punto 1 de la página 85 de exploradores.
El mínimo
común múltiplo (mcm) es el número más pequeño que es múltiplo de
dos o más números.
- Halla el m.c.m de 20 y 50, m.c.m de 15 y 26.
- Realiza el punto 1, 2 y 3 de la página 87.
- Realiza la página 229 de exploradores.
https://meet.google.com/tdd-jija-wdm?hs=122&authuser=2
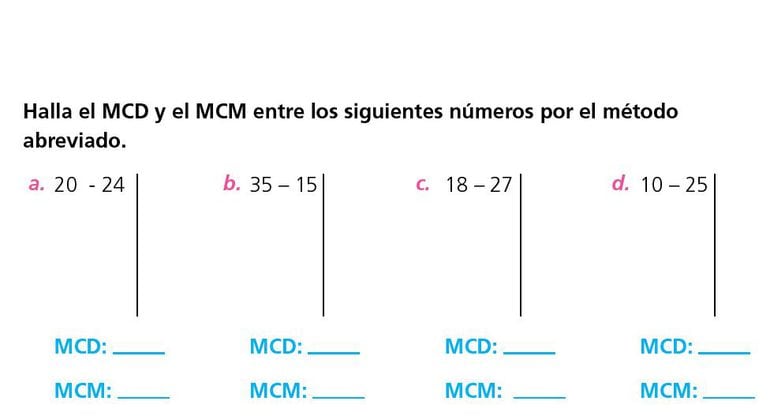
¿Qué es el Máximo Común Divisor (MCD)? Es el mayor número que divide exactamente a dos o más números.
Recordemos:
- Divisor: El divisor de
un número es el valor que divide al número en partes exactas, es decir, que el
resto sea cero.
- · Divisor Común: Es un número que es divisor a la vez de dos o más números, es decir, es un divisor común a esos números. Observando el ejemplo anterior vemos que los números que se repiten son el 1 y el 5.
- 12 y 24=
- 45 y 15=
- 65 y 35 =
- 14 y 32 =
https://meet.google.com/qtx-oybs-sza?hs=122&authuser=2
Recordemos:
Actividad #1: Realiza la página 89 y 230 de exploradores.
Tarea:
- El numerador es el número de partes que tenemos.
- El denominador es el número de partes en que hemos dividido la unidad.
- · Fracciones propias: Cuando el numerador es menor que el denominador.
- Fracciones impropias: Cuando el numerador es mayor que el denominador.
- Fracciones unitarias: Cuando el numerador es igual que el denominador.
https://meet.google.com/zif-zpgx-jft?hs=122&authuser=2
- 3/6 de 60 = (60/6 ) x3 =10 x 3 = 30
- 2/4 de 360 = ( 360/ 4 ) x 2 = 90 x 2 = 180
- 2/7 de 42=
- 5/6 de 36=
- 3/5 de 15=
- 3/9 de 72=
- 5/5 de 45=
https://meet.google.com/gka-bwea-yfr?hs=122&authuser=2
Actividad #2: Realiza la página 121 de exploradores.
https://meet.google.com/zzg-kiss-guo?hs=122&authuser=2
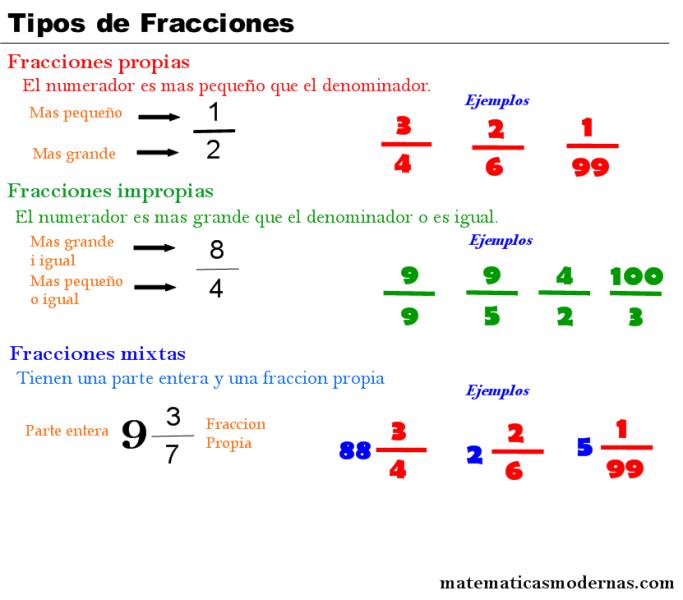
Tipos de fracciones:
- Fracciones propias: Cuando el numerador es menor que el denominador.
- Fracciones impropias: Cuando el numerador es mayor que el denominador.
- Fracciones unitarias: Cuando el numerador es igual que el denominador.
- Fracciones mixtas: Tienen una parte entera y una fracción.
https://meet.google.com/boq-yomk-chx?hs=122&authuser=2
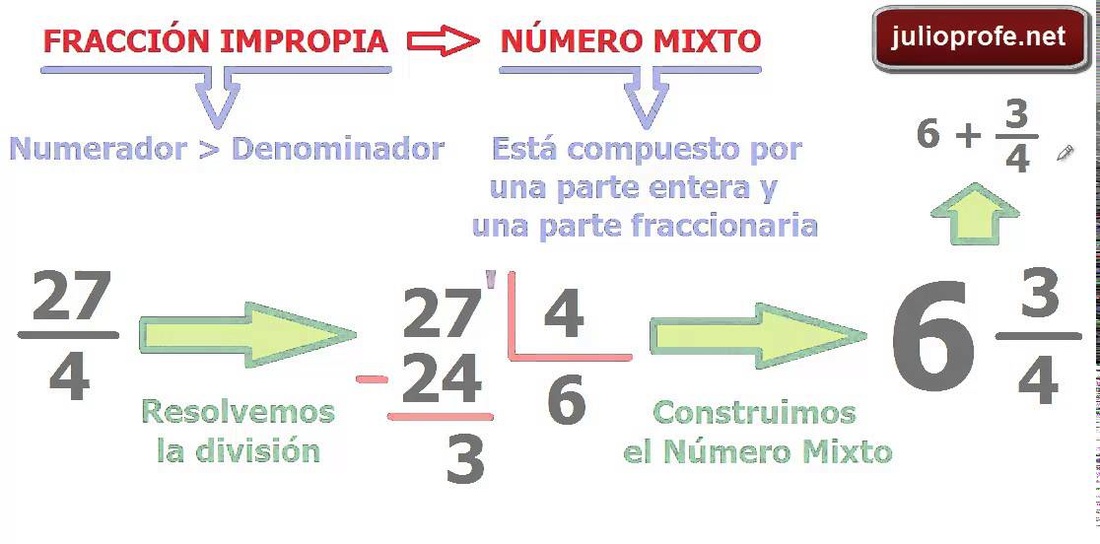
- Se divide el numerador por el denominador.
- El cociente de la división anterior se convierte en el entero del número mixto.
- El resto de la división es el numerador de la fracción.
- El denominador es el mismo que el de la fracción. Es el divisor de la división.
- Ejemplo:
- Se deja el mismo denominador
- El numerador es la suma de la multiplicación del entero por el denominador más el numerador del número mixto.
Taller de repaso
Lunes 31 de agosto de 2020
Comparación de Fracciones
https://meet.google.com/hks-acaz-feo?hs=122&authuser=2
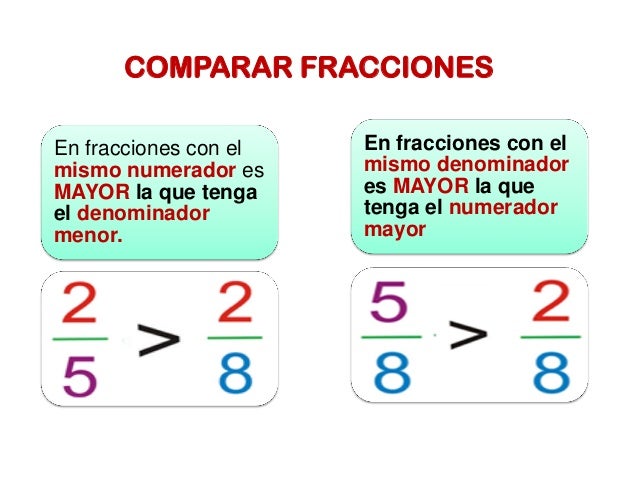
Comparar fracciones: A veces
tenemos que comparar dos fracciones para saber cuál es mayor y cuál es menor.
|
y
|
|
||||||||||||||||||||||||||||||||||||||
Comparación de Fracciones
https://meet.google.com/hdd-ubzk-pym?hs=122&authuser=2
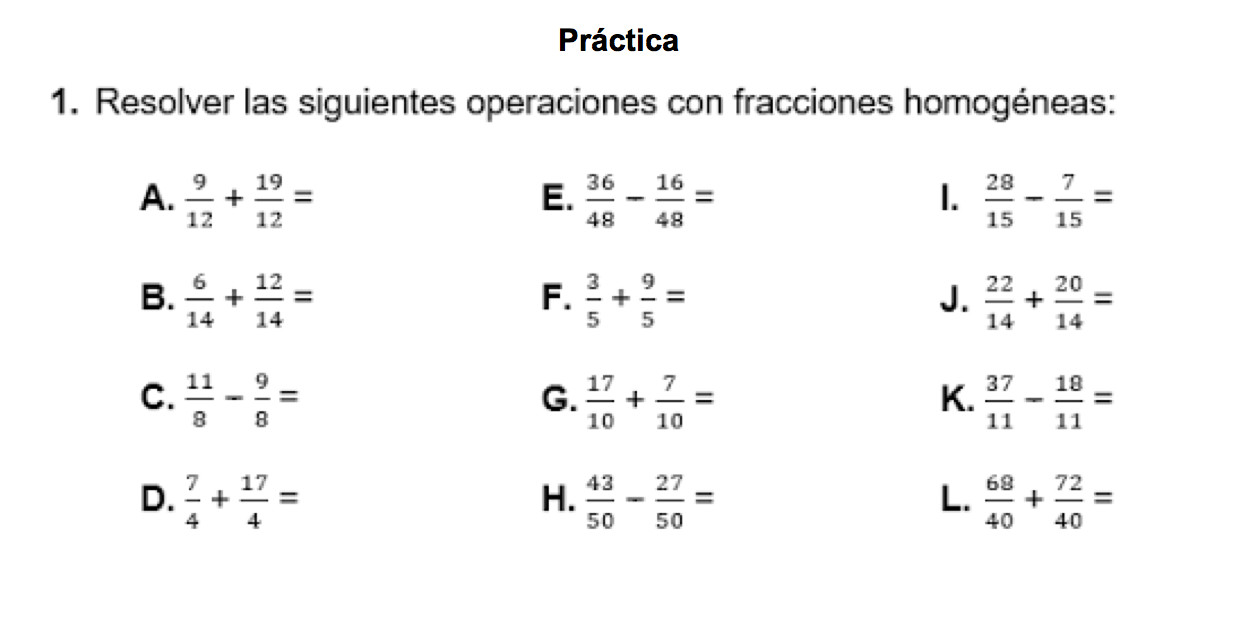
Suma y resta de fracciones homogéneas
https://meet.google.com/ryc-nfza-cbr?hs=122&authuser=2
- Paso 1: se suman o restan los numeradores (los números de arriba).
- Paso 2: los denominadores (números de abajo) se dejan igual.
- Paso 3: se simplifica la fracción (si es necesario).
Suma y resta de fracciones homogéneas
https://meet.google.com/jhx-wnih-scz?hs=122&authuser=2
Actividad #1:
Actividad #2: Realiza las páginas 129 y 244 de exploradores.
Tarea: Realiza la siguiente actividad
 Para
adicionar o restar fracciones con diferente denominador. Se buscan
fracciones equivalentes a las fracciones dadas, con igual denominador, es decir
se convierten en fracciones homogéneas y luego se suman o se restan.
Para
adicionar o restar fracciones con diferente denominador. Se buscan
fracciones equivalentes a las fracciones dadas, con igual denominador, es decir
se convierten en fracciones homogéneas y luego se suman o se restan.- Buscamos el mcm
- Buscamos fracciones equivalentes a las dadas de tal forma que el denominador sea mcm que se eligió y se complificar.
- Se suman o se restan las fracciones dadas. 5/6 y 3/4
- Se determina el mínimo común múltiplo (mcm) de los denominadores.
- Luego dividimos el denominador común (en este caso mcm (2,3,5,14)=210) por el denominador del primer término, y el resultado lo multiplicamos por el numerador. Repetimos la operación con cada una de las fracciones que tengamos. Por último se suman los resultados.
- 2/3+4/9=
- 4/5- 6/8 - 4/2=
- 6/4+ 5/8 + 6/6=
Miércoles 23 de septiembre de 2020
https://meet.google.com/phu-znub-xat?hs=122&authuser=2
ACTIVIDAD #1:Realiza los siguientes ejercicios:
https://meet.google.com/iqo-acsx-jai?hs=122&authuser=2
ACTIVIDAD #1: Realiza la página 132 de exploradores.
- 5/7 - 9/5
- 9/8 + 8/4 + 3/3
- 5/3 + 4/5
https://meet.google.com/dcj-fiqw-iit?hs=122&authuser=2
ACTIVIDAD #1: Realiza las páginas 133 y 245 de exploradores.
- 9/2 - 7/5
- 10/4 + 6/3 + 3/2
- 7/3 + 6/4
Para resolver este tipo de ejercicios:
1. Pasamos el número mixto a fraccionarios.
2. Como las fracciones tienen distinto denominador debemos calcular el m.c.m:
3. Realizar lo enseñado sobre la suma de fracciones heterogéneas.
Ejemplo: Recuerda cómo pasar un número mixto a fracción:
Multiplicación de fracciones
Ejemplo:
Actividad #1: Realiza las siguientes operaciones
Para dividir dos o más fracciones, se multiplican "en cruz". Esto es: el numerador (número de arriba) de la primera fracción por el denominador (número de abajo) de la segunda fracción, así conseguimos el numerador. Para obtener el denominador, tenemos que multiplicar el denominador (número de abajo) de la primera fracción por el numerador (número de arriba) de la segunda fracción.
Actividad #1: Realiza los siguientes ejercicios:- 4/6 : 3/2
- 9/3 :4/6
- 7/9: 6/5
Actividad #2: Realiza las páginas 140 y 141 de exploradores.
Miércoles 04 de Noviembre de 2020Unidades de longitud
Ingresa al siguiente link para la videoconferencia:
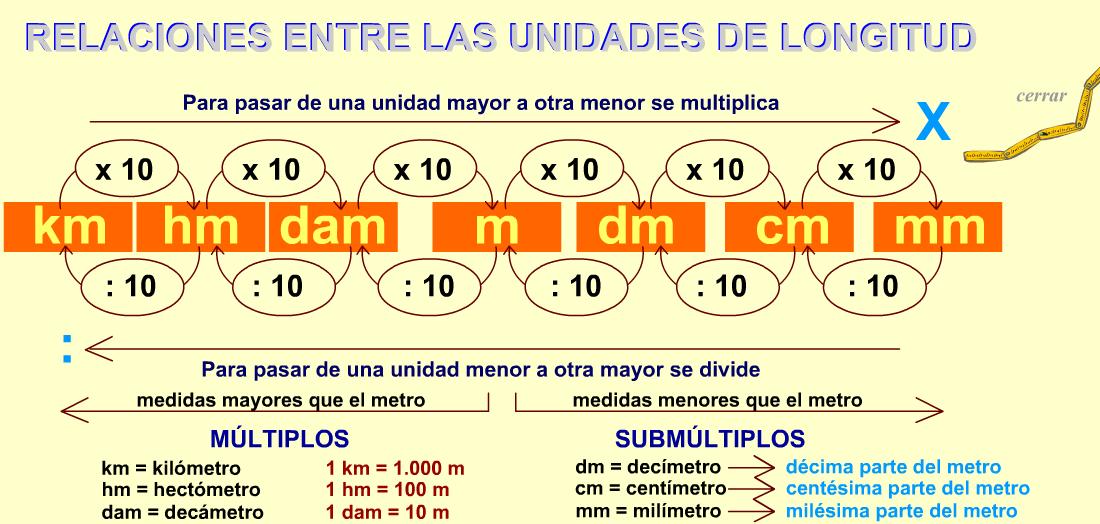
La longitud es la distancia que une 2 puntos y, a través de la longitud se obtiene la longitud vertical, es lo que se conoce como altura y, de tomarse en cuenta una longitud horizontal es sinónimo de ancho.La unidad de medida de longitud es el metro. El Sistema Métrico Decimal, está compuesto de la siguiente manera: longitudes menores al metro son: decímetro, centímetro, milímetro y, las longitudes mayores al metro son: decámetro, hectómetro, kilómetro y miriámetro.
Conversiones
Para realizar conversiones con las unidades de longitud debemos multiplicar o dividir por 10, 100 o 1000 según los saltos que se den de una medida a otra. - Si van de una unidad mayor a una menor se debe multiplicar.
- Si se va de una unidad menor a una mayor se debe dividir.
Actividad #1: Realiza las siguientes conversiones- 3 metros a decímetros.
- 28 metros a centímetros.
- 543 milimetros a decametros.
Actividad #2: Realiza el siguiente taller:
Tarea: Realiza la página 143 de exploradores.
Lunes 9 de Noviembre de 2020Unidades de longitud
Ingresa al siguiente link para la videoconferencia:
Actividad #1: Realiza las siguientes conversiones:- 67 Hm a m
- 98 dm a mm
- 32 m a Dam
- 94 km a Dam
- 20 mm a cm
- 800 cm a m
Tarea: Realiza las páginas 143 y 249 de exploradores.
Miércoles 11 de Noviembre de 2020Taller de repaso
Ingresa al siguiente link para la videoconferencia:
Realiza el siguiente taller:
- 4/6 : 3/2
- 9/3 :4/6
- 7/9: 6/5
- Si van de una unidad mayor a una menor se debe multiplicar.
- Si se va de una unidad menor a una mayor se debe dividir.
- 3 metros a decímetros.
- 28 metros a centímetros.
- 543 milimetros a decametros.
- 67 Hm a m
- 98 dm a mm
- 32 m a Dam
- 94 km a Dam
- 20 mm a cm
- 800 cm a m






















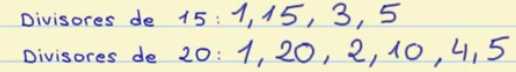



.png)





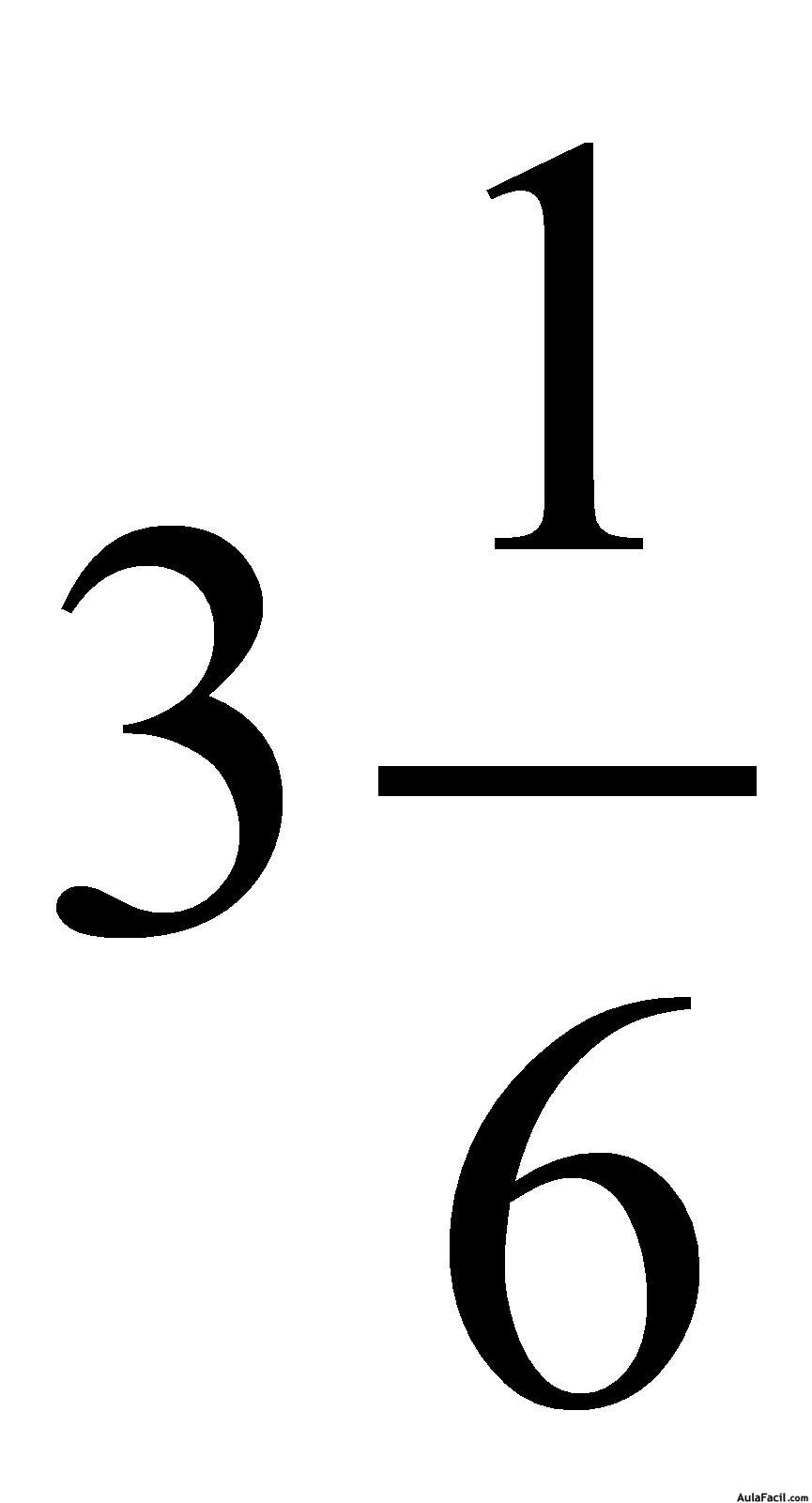
























Hacer divisiones rapido
ResponderEliminaraprender las tablas al derecho y al revés y mejorar mi velocidad haciendo divisiones
ResponderEliminar