13 de abril de 2020
Los fraccionarios
ingresar al siguiente link
Recordemos información sobre las fracciones
Para practicar un poco, realicemos la página 69 del libro exploradores.
Fracciones equivalentes
Son aquellas fracciones que representan una misma cantidad, aunque el
numerador y el denominador sean diferentes.
¿Por qué es lo mismo? Porque cuando
multiplicas o divide a la vez arriba y abajo por el mismo
número, la fracción mantiene su valor.
Simplificación: (dividimos el numerador y el denominador por el mismo número).
complificación: (Multiplicamos el numerador y el denominador por el mismo número).
¿Cómo saber si dos fracciones son equivalentes?
Cuando quiero saber si dos fracciones son equivalentes,
puedo realizar "producto cruzado": Multiplico al
numerador de la primera fracción por el denominador de la segunda fracción y
escribo el producto sobre la primera fracción. Luego multiplico el otro
numerador por el otro denominador y escribo el producto sobre la
segunda fracción. Si ambos productos son iguales, las fracciones son
equivalentes.
Para practicar un poco, realicemos la página 71 del libro exploradores.
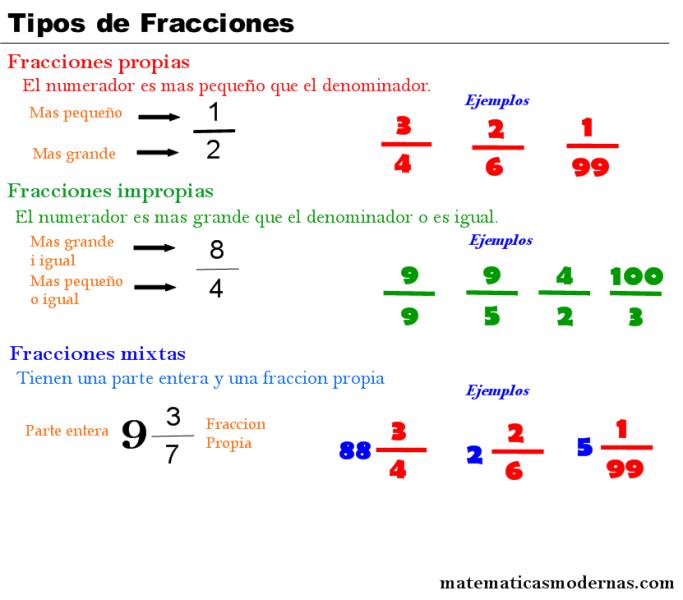
Tipos de fracciones
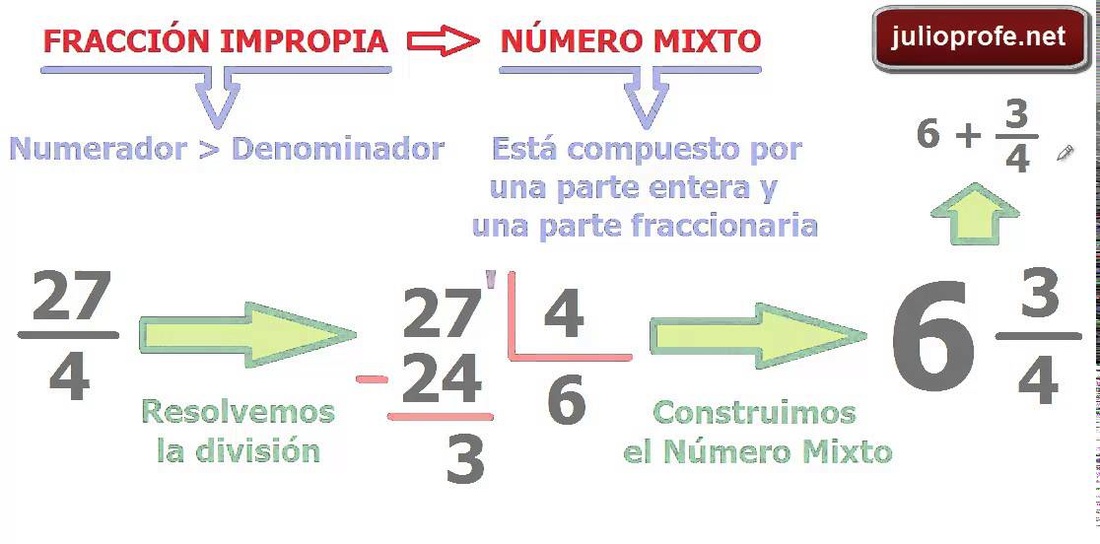
¿Cómo pasar una fracción impropia a número mixto?
Pasar de fracción a número mixto.
- Se divide el numerador por el denominador.
- El cociente de la división anterior se convierte en el entero del número mixto.
- El resto de la división es el numerador de la fracción.
- El denominador es el mismo que el de la fracción. Es el divisor de la división.
- Ejemplo:
¿Cómo pasar un número mixto a fracción impropia?
¡Practiquemos un poco!
Pasa las siguientes fracciones a número mixto
Pasa los siguientes números mixtos a fracciones impropias.
Tarea: Realiza la página 73 del libro exploradores.
15 de abril de 2020
Comparación de fracciones
Únete al video de la conferencia con el siguiente link: https://meet.google.com/gwb-wtcs-kzr?hs=122&authuser=1
Recordemos:
¡Practiquemos un poco!
Realicemos entre todos las páginas 221 y 75.
Tarea: Realiza la página 222.
20 de abril de 2020
Únete a la videoconferencia con el siguiente link:
Suma y resta de fracciones heterogéneas
Recuerda cómo obtener el M.C.M
Suma de números mixtos con distinto
denominador
Para
resolver este tipo de ejercicios:
- Pasamos el número mixto a fraccionario.
- Como las fracciones tienen distinto denominador debemos calcular el m.c.m.
- Luego realiza lo enseñado sobre la suma y resta de fracciones heterogéneas.
Observa el siguiente video explicativo
Teniendo en cuenta el video visto, realiza los siguientes ejercicios en tu cuaderno y enviame una foto a mi whatsApp.
Tarea: Realiza las páginas 77 y 223.
22 de abril de 2020
Únete al video de la conferencia con el siguiente link:
División y multiplicación de fraccionarios
Actividad: Realiza las páginas 79 y 81 del libro de exploradores.
Tarea: Realiza la página 224 y 225 de exploradores.
4 de mayo de 2020
Polinomios aritméticos con fracciones
Ingresa al siguiente link para iniciar la videoconferencia:
Recuerda el orden que debemos seguir al resolver polinomios aritméticos u operaciones combinadas:
Ahora recordemos las operaciones entre fracciones
Suma y resta:
Multiplicación:
División:
Observemos un ejemplo:
Observa el siguiente video y presta atención a su solución:
Actividad: Soluciona la página 83 del libro exploradores.
Tarea: Practica la solución de polinomios realizando la página 226 del libro exploradores.
06 de mayo de 2020
Ejercicios polinomios
Ingresa al siguiente link para unirte a la videoconferencia:
Realiza los siguientes ejercicios:
11 de mayo de 2020
Ingresa al siguiente link para la videoconferencia:
Ejercicios polinomios
Resuelve los siguientes polinomios:
Ahora, realiza las páginas 85, 86, 87 de exploradores.
Tarea: Realiza la página 227 de exploradores.
13 de mayo de 2020
Ingresa al siguiente link para la videoconferencia:
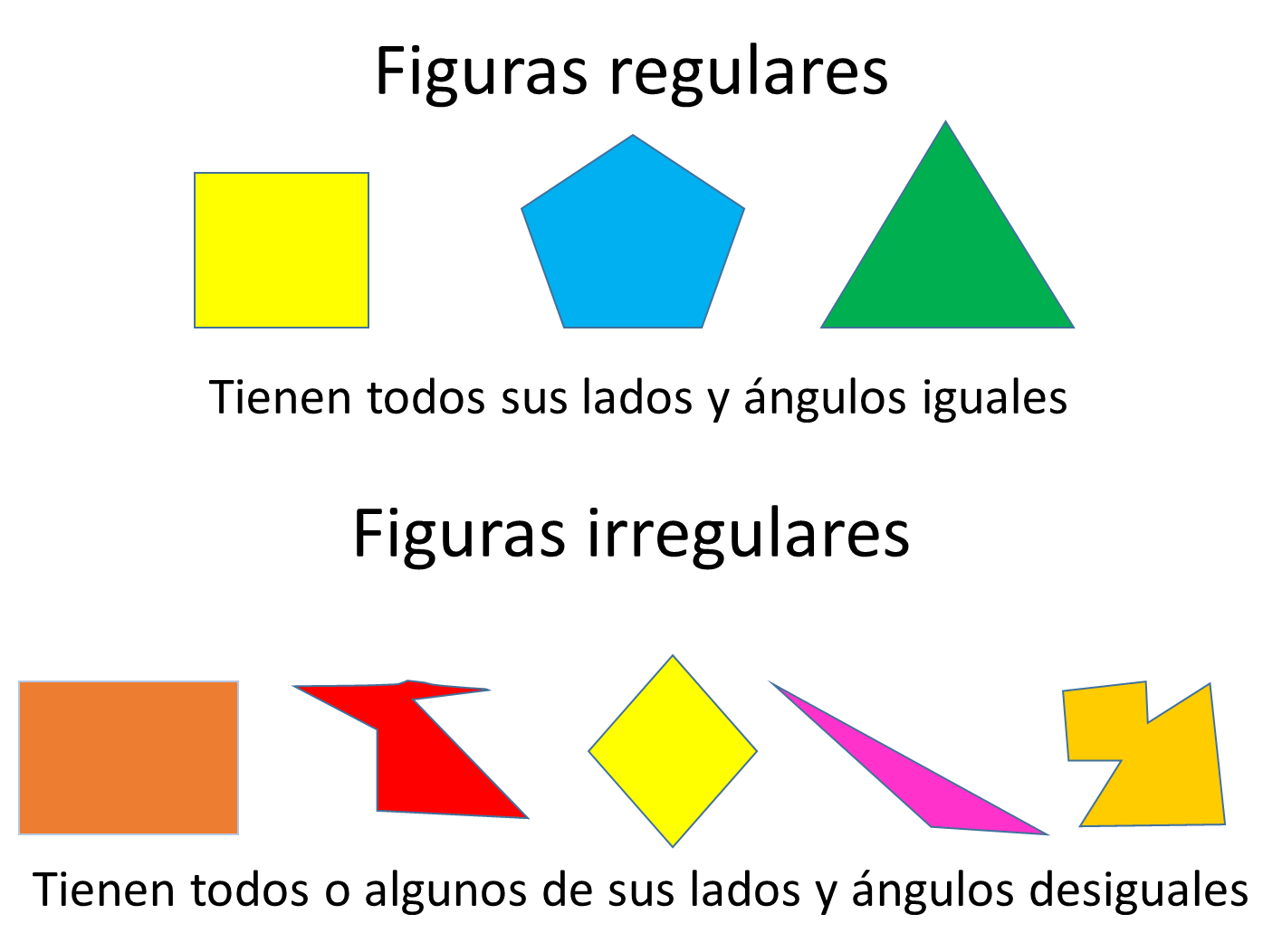
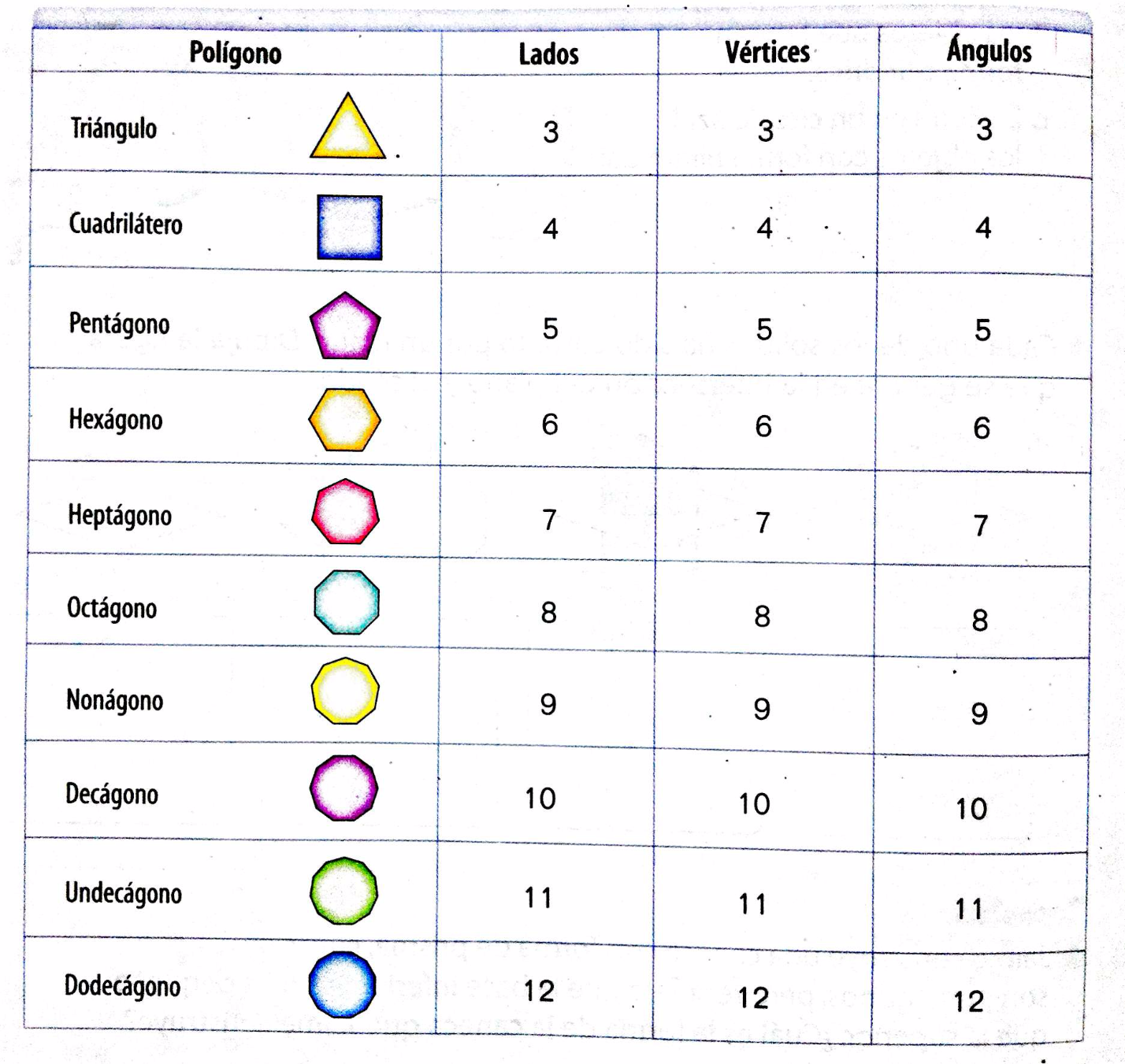
Los polígonos son figuras en un plano que pueden estar representadas de diferentes formas y maneras. El polígono está compuesto de líneas que no deben ser curvas cerradas (es por eso que un círculo no es considerado como un polígono).
También pueden estar clasificados según su número de lados
¡JUGUEMOS!
Actividad #1: Ingresa al siguiente link y realiza la actividad:
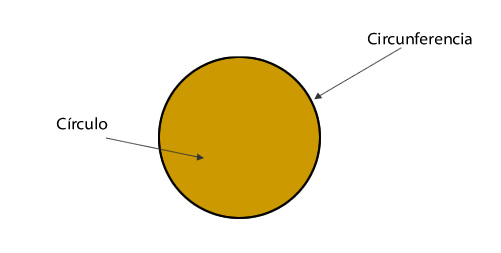
El círculo y la circunferencia
La circunferencia
La circunferencia es una línea curva cerrada y plana cuyos puntos están a igual distancia de otro fijo, llamado centro. Para dibujar circunferencias utilizamos el compás.
Ejemplos de circunferencia: anillo, aro.
Círculo
Es una figura plana limitada por una circunferencia. Está formado por la circunferencia y la parte de plano que hay dentro de ella.
Ejemplos de círculo: moneda, disco
Elementos de una circunferencia
- Centro punto del interior de la circunferencia tal que la distancia desde él a cualquier punto de la circunferencia es la misma.
- Radio es el segmento que une el centro con cualquier punto de la circunferencia.
- Diámetro es el segmento que tiene por extremos dos puntos de la circunferencia y que pasa por el centro. El diámetro es el doble del radio. D = 2·R
- Cuerda es el segmento que une dos puntos cuales quiera de la circunferencia. La cuerda mayor de una circunferencia es el diámetro.
- Arco parte de la circunferencia comprendida entre dos puntos.
- Semicircunferencia es cada una de las partes en que un diámetro divide a una circunferencia, es decir, media circunferencia.
¿Cómo encontrar el radio y el diámetro?
Radio: La forma más sencilla de hallar el radio es dividir el diámetro a la mitad.
Diámetro: Se encuentra multiplicando el radio x2.
¡Practiquemos!
Actividad #2: Para practicar un poco, ingresa al siguiente enlace:
http://www.accede-tic.es/circuloycircunferencia/elementos.html, realiza la actividad y envíame evidencia.
Tarea:
1. Encuentra el radio o el diámetro de las siguientes medidas:
1. Encuentra el radio o el diámetro de las siguientes medidas:
- D=54cm R=?
- D=440cm R=?
- D=? R=34cm
- D=? R=93cm
Lunes 18 de mayo de 2020
Tablas de frecuencia y medidas de tendencia central (moda, mediana y media)
Ingresa al siguiente link para la videoconferencia:
Actividad #1: realiza las páginas 91 y 228.
Tabla de datos o de frecuencia
La frecuencia de un dato es el número de veces que ese dato se repite y estos datos los podemos organizar en una tabla de datos o tabla de frecuencia.
Medidas de tendencia central
Las Medidas de tendencia central son
medidas que se utilizan en la estadística para resumir información. Para poderlas realizar se necesita una
tabla de datos o de frecuencia (valores).
Las
medidas de tendencia son tres:
a) Media
o promedio
b) Moda
c) Mediana
Media aritmética o promedio
Consiste
en hallar un número medio entre varios de la misma especie. Es una cantidad que nos indica la cantidad total dividida en
partes iguales. Se identifica con
las letras M o X.
Para hallar la
media aritmética o promedio de varias cantidades, se suman todos los datos y
esta suma se divide por el total de datos.
Ejemplo: Hallar la media aritmética o promedio de las
siguientes cantidades (estos son los datos o valores): 9, 10, 4, 6, 9, 6, 8, 9,
1, 9, 6, 9, 4.
- Primero sumo todas las cantidades anteriores: 9 +10 + 4 + 6 + 9 + 6 + 8 + 9 + 1 + 9 + 6 + 9 + 4 = 90
- El resultado de la suma se divide entre el total de los números sumados: 90 ÷ 13 = 6.9
- M=6.9
Moda
Esta medida consiste en encontrar un dato o
valor que se repite más veces en el conjunto de valores dados. Es decir, el
valor que tiene mayor frecuencia. Se
identifica con las letras Mo
Ejemplo: En el conjunto
9, 10, 4, 6, 9, 6, 8, 9, 1, 9, 6, 9, 4
la moda es 9 porque es el valor con mayor frecuencia (el que más se
repite). Mo = 9
Si en un grupo de datos o valores hay dos con
la misma frecuencia, entonces se dice que es bimodal.
Ejemplo: En el
conjunto 9,10,4,6,9, 6, 8, 9, 1, 9, 6, 9, 4, 6, 6 La frecuencia de 9 y 6 es igual (cinco veces cada uno) y es la mayor (es decir los valores que más
se repiten), por lo tanto es bimodal.
Mo
bimodal = 9 y 6
Si hubiera más de tres datos con la mayor e
igual frecuencia, entonces sería multimodal.
Ejemplo: Si en el conjunto anterior hubiera tres cuatros más, entonces, el 9, el 6 y el 4 tendrían la misma
frecuencia y la más alta, por lo tanto la moda sería multimodal. 9, 10, 4, 6,
9, 6, 8, 9, 1, 9, 6, 9, 4, 6, 6, 4, 4, 4
Mo multimodal = 9, 6, 4
Mediana
Consiste en hallar el valor que se encuentra en
el centro del conjunto de datos o valores. Para encontrarla, la condición es
que los datos estén ordenados del menor al mayor. Se identifica con las letras Md
Se pueden dar dos casos.
1.- Cuando el número total de valores es impar. En este
caso, después de ordenar los valores de menor a mayor, la mediana es el valor que
queda al centro de la serie.
Ejemplo:
Encontrar la mediana del conjunto: 9, 10, 4, 6, 9, 6, 8, ,9, 1, 9, 6, 9, 4.
- Primero hay que ordenarlos de menor a mayor: 1, 4, 4, 6, 6, 6, 8, ,9, 9, 9, 9, 9, 10.
- Se cuentan los datos, en este caso son trece valores, el trece es impar.
- Ahora, se debe localizar el que se encuentra en el centro.
- Quedan seis datos antes del centro y seis después. 1, 4, 4, 6, 6, 6, 8, 9, 9, 9, 9, 9, 10
- La mediana de este conjunto es 8. Md = 8
2.- Cuando el número total de valores es par. En este
caso se localizan los dos valores que quedan al centro, se suman y el resultado
se divide entre dos (es decir, se promedian los dos valores) para encontrar la
mediana.
Ejemplo. En el conjunto 9,
10, 4, 6, 9, 6, 8, ,9, 1, 9, 6, 9, 4, 6 Los datos del conjunto son catorce (que
es número par), entonces:
- Ordeno de mayor a menor y busco los dos que quedan al centro de la serie 1, 4, 4, 6, 6, 6, 8, 9, 9, 9, 9, 9, 10,6.
- Ahora saco el promedio de 8 y 9
- 8 + 9 = 17 ÷ 2 = 8.5
- La mediana es 8.5 Md = 8.5
Actividad #2: Consigue la edad de los padres de todos tus compañeros de clase, elabora una tabla de frecuencia y a los datos sacale la moda, la mediana y la media.
Cómo pasar de fracción a decimal
Miércoles 20 de mayo de 2020
Tablas de frecuencia y medidas de tendencia central (moda, mediana y media)
Ingresa al siguiente link para la videoconferencia:
Recuerda la información vista sobre, moda, mediana y media:
Ahora, realiza las páginas 99, 101 y 103.
Tarea: 231,232 y 233.
Miércoles 27 de mayo de 2020
Resolución de problemas
Ingresa al siguiente link y únete a la reunión:
Actividad: Realiza las páginas 104 y 105.
Lunes 01 de junio de 2020
Fracciones y expresiones decimales
Ingresa al siguiente link y únete a la reunión:
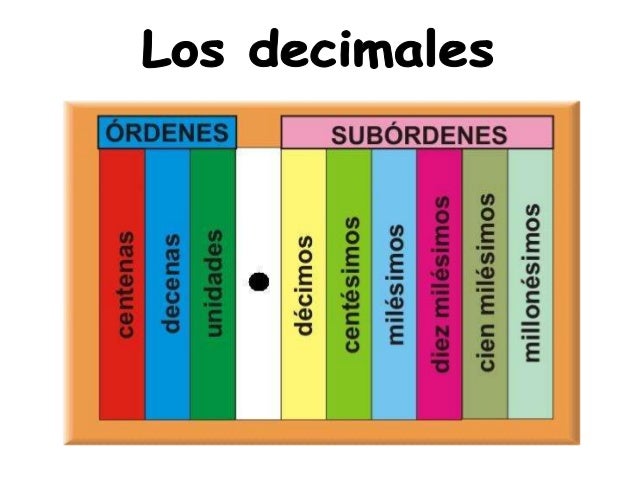
Los números decimales se utilizan para representar números más pequeños que la unidad. Los números decimales se escriben a la derecha de las Unidades separados por una coma. Es decir: Centenas Decenas Unidades , Décimas Centésimas Milésimas.
Lectura de números decimales
¿Cuál es la relación de los decimales con las
fracciones?
- La Unidad se representa por 1
- La Décima es la unidad dividida en 10 partes iguales = 1/10 = 0,1
- La Centésima es la unidad dividida en 100 partes iguales = 1/100 = 0,01
- La Milésima es la unidad dividida en 1000 partes iguales = 1/1000 = 0,001
Cómo pasar de decimal a fracción
7,508 Nos fijamos en el último número, en el 8, que ocupa el
lugar de las milésimas, por lo tanto el denominador tendrá que ser 1000. Y en
el numerador escribiremos el número completo sin la coma. 7,508 = 7508/1000
Cómo pasar de fracción a decimal
402/100 Como el denominador es 100, el último número del
numerador (el 2) , tiene que ser las centésimas, el anterior (el 0) tienen que
ser las décimas y el anterior a éste (el 4) tiene que ser las unidades, poniendo la coma detrás de las
unidades. Por lo tanto, 402/100 = 4,02
Practiquemos
1. Escribe el nombre de los siguientes decimales.
2. Pasa los siguientes decimales a fracciones:
3. Ingresa al siguiente link y responde una ronda de preguntas completas, cuando termines, enviame la evidencia:
Miércoles 03 de junio de 2020
Fracciones y expresiones decimales
Ingresa al siguiente link y únete a la reunión:
¡Practiquemos!
Realiza las páginas 115 y 117.
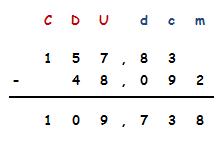
Suma y resta de decimales
Para sumar o restar decimales se
colocan los números decimales uno debajo del otro, haciendo que coincidan las
unidades en la misma columna. De esta manera, también tienen que
coincidir las décimas, las centésimas… y la coma.
Ejemplo:
Suma:
Resta:
Tarea: Realiza las páginas 234 y 235 de exploradores.
Lunes 08 de junio del 2020
Suma y resta de decimales
Ingresa al siguente link y únete a la videollamada:
Actividad #1: Realiza las páginas 119 y 236 de exploradores.
Miércoles 10 de junio del 2020
Miércoles 10 de junio del 2020
Multiplicación de decimales
Ingresa al siguente link y únete a la videollamada:
Para multiplicar un número decimal por un número entero, se multiplica como si el número decimal fuera un número entero. En el resultado se separan tantas cifras decimales como tenía el número decimal.
¡Practiquemos!
Realiza los siguientes ejercicios:
Miércoles 17 de junio del 2020
Multiplicación de decimales
Ingresa al siguente link y únete a la videollamada:
https://meet.google.com/gkv-kgkv-qji?hs=122&authuser=2
Actividad:
https://meet.google.com/gkv-kgkv-qji?hs=122&authuser=2
Actividad:
- Realiza el punto 1 de la página 121.
- realiza los puntos 1 y 3 de la página 123.
División de decimales
Miércoles 24 de junio del 2020
División de decimales con naturales
Ingresa al siguente link y únete a la videollamada:
https://meet.google.com/ood-dtaf-rve?hs=122&authuser=2
Actividad # 1: Realiza las siguientes divisiones
Actividad # 2:Ingresa al siguiente link y practiquemos:https://meet.google.com/ood-dtaf-rve?hs=122&authuser=2
Observa el siguiente video
Actividad # 1: Realiza las siguientes divisiones
- 45,23 / 23
- 984,23/2
- 2,34/5
Tarea: Realiza las siguientes divisiones
- 38,3/26
- 105,27/53
- 1,63/3
Miércoles 01 de julio del 2020
División de natural con decimal
Ingresa al siguente link y únete a la videollamada:
https://meet.google.com/vdf-mtqj-dgk?hs=122&authuser=2
Actividad # 1: Realiza las siguientes divisiones
https://meet.google.com/vdf-mtqj-dgk?hs=122&authuser=2
Observa el siguiente video
- 543/3,2
- 7632/23,6
- 987/3,4
Tarea: Realiza las siguientes divisiones
- 875/5,2
- 9876/21,7
- 543/1,4
Lunes 06 de julio del 2020
División de decimal con decimal
Ingresa al siguente link y únete a la videollamada:
https://meet.google.com/cwa-vbri-qmz?hs=122&authuser=2
Actividad # 1: Realiza las siguientes divisiones
https://meet.google.com/cwa-vbri-qmz?hs=122&authuser=2
Observa el siguiente video
Actividad # 1: Realiza las siguientes divisiones
- 45,43/3,2
- 76,322/2,36
- 9,87/3,4
Tarea:
- Realiza las siguientes divisiones
- 83,75/5,2
- 3,9876/2,17
- 5,43/1,4
2. Realiza la página 125 de exploradores.
Miércoles 08 de julio del 2020
División de decimales
Ingresa al siguente link y únete a la videollamada:
https://meet.google.com/sfo-hqfu-nsf?hs=122&authuser=2
Recordemos:
ACTIVIDAD #1: Realiza la página 127 de exploradores.
Tarea:
https://meet.google.com/sfo-hqfu-nsf?hs=122&authuser=2
Recordemos:
ACTIVIDAD #1: Realiza la página 127 de exploradores.
Tarea:
- Realiza el punto 1 de la página 239 de exploradores.
- Realiza el punto 1 y 2 de la página 240 de exploradores.
Miércoles 22 de julio del 2020
Multiplicación de decimales por 10, 100 y 1000
Ingresa al siguente link y únete a la videollamada:
https://meet.google.com/fzb-kowf-xdp?hs=122&authuser=2
Para multiplicar un número decimal por la unidad seguida de ceros (10; 100; 1000...) se desplaza la coma hacia la DERECHA tantos lugares como ceros acompañen a la unidad. Si no hay espacios suficientes, agregamos ceros.
Ejemplos:
¡Intentalo tu!
Realiza las siguientes multiplicaciones abreviadas:
Lunes 27 de julio del 2020
https://meet.google.com/fzb-kowf-xdp?hs=122&authuser=2
Para multiplicar un número decimal por la unidad seguida de ceros (10; 100; 1000...) se desplaza la coma hacia la DERECHA tantos lugares como ceros acompañen a la unidad. Si no hay espacios suficientes, agregamos ceros.
Ejemplos:
¡Intentalo tu!
Realiza las siguientes multiplicaciones abreviadas:
- 34,56 x 10 =
- 56,234 x 1000 =
- 3,4 x 100 =
Tarea: Realiza las siguientes multiplicaciones abreviadas:
- 45,64 x 10 =
- 76,765 x 100 =
- 3,4 x 1000 =
- 76,543 x 1000 =
- 45,6 x 100 =
- 0,34 x 10=
Lunes 27 de julio del 2020
División de decimales por 10, 100 y 1000
Ingresa al siguente link y únete a la videollamada:
https://meet.google.com/omq-zmzo-xzq?hs=122&authuser=2
Para Dividir un número decimal por la unidad seguida de ceros (10; 100; 1000...) se desplaza la coma hacia la IZQUIERDA tantos lugares como ceros acompañen a la unidad. Si no hay espacios suficientes, agregamos ceros.
Ejemplos:
¡Intentalo tu!
Actividad #1: Realiza las siguientes divisiones abreviadas:
https://meet.google.com/omq-zmzo-xzq?hs=122&authuser=2
Para Dividir un número decimal por la unidad seguida de ceros (10; 100; 1000...) se desplaza la coma hacia la IZQUIERDA tantos lugares como ceros acompañen a la unidad. Si no hay espacios suficientes, agregamos ceros.
Ejemplos:
Actividad #1: Realiza las siguientes divisiones abreviadas:
- 34,56 /10 =
- 56,234 / 1000 =
- 3,4 / 100 =
- 45,64 / 10 =
- 76,765 / 100 =
Actividad #2: Realiza las páginas 129 y 241 de exploradores.
Tarea: Realiza las siguientes divisiones abreviadas.
Miércoles 29 de julio del 2020
División y multiplicación de decimales por 10, 100 y 1000
Ingresa al siguente link y únete a la videollamada:
https://meet.google.com/aih-yvjs-uar?hs=122&authuser=2
https://meet.google.com/aih-yvjs-uar?hs=122&authuser=2
Recuerda...
Actividad: Realiza las páginas 130 y 131 de exploradores.
Lunes 03 de agosto de 2020
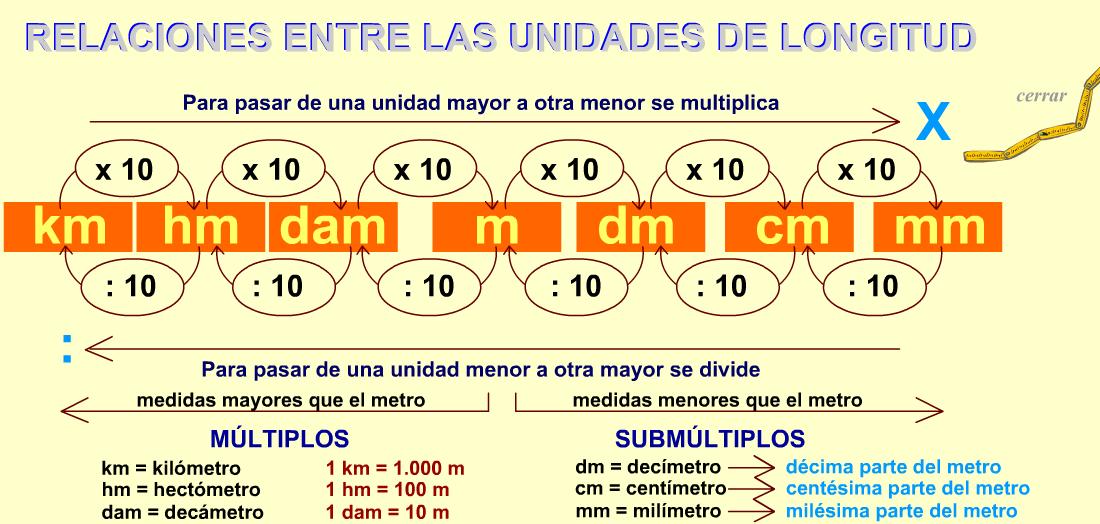
Unidades de longitud

Observamos
que desde los submúltiplos, en la parte inferior, hasta los múltiplos, en la
parte superior, cada unidad vale 100 más que la anterior. Por lo
tanto, el problema de convertir unas unidades en otras se reduce a multiplicar
o dividir por la unidad seguida de tantos pares de ceros como lugares haya
entre ellas.
Ingresa al siguente link y únete a la videollamada:
La longitud es la distancia que une 2 puntos y, a través de la longitud se obtiene la longitud vertical, es lo que se conoce como altura y, de tomarse en cuenta una longitud horizontal es sinónimo de ancho.
La unidad de medida de longitud es el metro. El Sistema Métrico Decimal, está compuesto de la siguiente manera: longitudes menores al metro son: decímetro, centímetro, milímetro y, las longitudes mayores al metro son: decámetro, hectómetro, kilómetro y miriámetro.
Para realizar conversiones con las unidades de longitud debemos multiplicar o dividir por 10, 100 o 1000 según los saltos que se den de una medida a otra.
- Si van de una unidad mayor a una menor se debe multiplicar.
- Si se va de una unidad menor a una mayor se debe dividir.
Actividad #1: Realiza las siguientes conversiones
- 3 metros a decímetros.
- 2,8 metros a centímetros.
- 543 milimetros a decametros.
Actividad #2: Realiza el siguiente taller:
Actividad #3: Realiza la página 133 de exploradores.
Tarea: Realiza la página 242 de exploradores.
Miércoles 05 de agosto de 2020
Unidades de longitud
Ingresa al siguente link y únete a la videollamada:
Actividad #1: Realiza la página 135 de exploradores.
Tarea: Realiza la página 243 de exploradores.
Lunes 10 de agosto de 2020
Unidades de superficie
Ingresa al siguente link y únete a la videollamada:
La porción del plano que
ocupan las figuras se denomina superficie. La medida de esa superficie se llama
área. La medida del área de una superficie depende de la unidad elegida, se
mide en unidades cuadradas de longitud.
kilómetro cuadrado
|
km2
|
1 000 000 m2
|
|||
hectómetro cuadrado
|
hm2
|
10 000 m2
|
|||
decámetro cuadrado
|
dam2
|
100 m2
|
|||
metro cuadrado
|
m2
|
1 m2
|
|||
decímetro cuadrado
|
dm2
|
0.01 m2
|
|||
centímetro
cuadrado
|
cm2
|
0.0001 m2
|
|||
milímetro
cuadrado
|
mm2
|
0.000001 m2
|
|||
La unidad principal de superficie es el metro
cuadrado.
Otras unidades
mayores y menores son:
Conversión de unidades
Pasar 1.5 Hm2 a
m2: Tenemos que multiplicar, porque el Hm2 es
mayor que el m2; por la unidad seguida de cuatro ceros, ya
que hay dos lugares entre ambos. 1.5 · 10 000 = 15 000 m2
Pasar 15 000 mm2 a m2: Tenemos que dividir,
porque el mm2 es menor que el m2, por la
unidad seguida de seis ceros, ya que hay tres lugares entre ambos. 15.000 :
1 000 000 = 0.015 m2
Practiquemos:
Realiza las siguientes conversiones:
Miércoles 12 de agosto de 2020
Unidades de superficie
Ingresa al siguente link y únete a la videollamada:
Actividad: Realiza las páginas 137 y 244 de exploradores.
Tarea: Realiza el siguiente taller
Miércoles 19 de agosto de 2020
El área
Unidades de superficie
Miércoles 26 de agosto de 2020
https://meet.google.com/hei-krne-sfp?hs=122&authuser=2
Ingresa al siguiente link y únete a la videollamada:
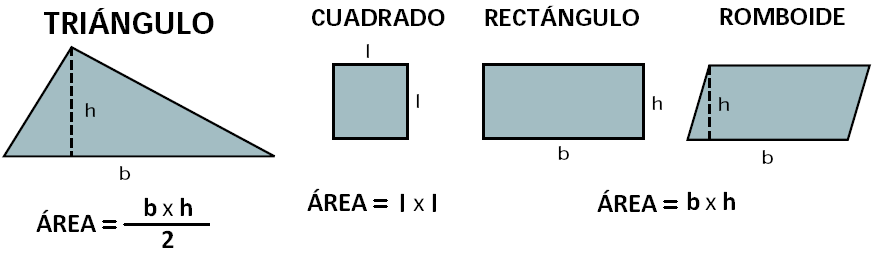
El Área de una Figura Geométrica es el espacio que queda encerrado entre los límites de esa figura. Para calcular el área de algunas de las figuras geométricas utilizamos una serie de fórmulas.
La medida del área de una figura se da en unidades cuadradas.
Observa algunas formulas de para hallar el área de las figuras geométricas
- Área de un triángulo = b x h / 2
- Área del cuadrado= l 2
- Área de un rectángulo= b x h
Lunes 24 de agosto de 2020
Repaso
Ingresa al siguiente link y únete a la videollamada:
https://meet.google.com/hei-krne-sfp?hs=122&authuser=2Miércoles 26 de agosto de 2020
El área
Unidades de superficie
Ingresa al siguiente link y únete a la videollamada:
https://meet.google.com/hei-krne-sfp?hs=122&authuser=2
Recuerda
Actividad #1: Encuentra el área de las siguientes figuras:
Actividad #2: Realiza la página 139 de exploradores.
Actividad #2: Realiza la página 139 de exploradores.
Lunes 31 de agosto de 2020
El área
Unidades de superficie
Ingresa al siguiente link y únete a la videollamada:
https://meet.google.com/xtm-khcs-mva?hs=122&authuser=2
Actividad #1: Resuelve los siguientes problemas:
Actividad #2:Realiza la página 245 de exploradores.
Actividad #1: Realiza las páginas 141 y 246 de exploradores.
https://meet.google.com/mra-vjef-axr?hs=122&authuser=2
Actividad #1: Ingresa al siguiente link: http://www.juntadeandalucia.es/averroes/centros-tic/41009470/helvia/aula/archivos/repositorio/0/193/html/recursos/la/U14/pages/recursos/143304_P197/es_carcasa.html
Actividad #2:Realiza las páginas 143 y 247 del libro exploradores.
https://meet.google.com/xtm-khcs-mva?hs=122&authuser=2
Actividad #1: Resuelve los siguientes problemas:
- Calcula el número de baldosas cuadradas que hay en un salon rectangular de 6 m de largo y 4,5 m de ancho, si cada baldosa mide 30 cm de lado.
- Calcula cuál es el precio de un mantel cuadrado de 3,5 m de lado si el m2 de tela cuesta 1.200 pesos.
Actividad #2:Realiza la página 245 de exploradores.
Miércoles 02 de Septiembre de 2020
Área
Ingresa al siguiente link y únete a la videollamada:
https://meet.google.com/bog-rtat-zni?hs=122&authuser=2
https://meet.google.com/bog-rtat-zni?hs=122&authuser=2
Lunes 07 de Septiembre de 2020
Prismas y pirámides
Ingresa al siguiente link y únete a la videollamada:
Miércoles 09 de Septiembre de 2020
Prismas y pirámides
Ingresa al siguiente link y únete a la videollamada:
Actividad #1: Resuelve el siguiente taller:
Lunes 14 de Septiembre de 2020
Cilindros, conos y esferas
Ingresa al siguiente link y únete a la videollamada:
Actividad #1: Ingresa al siguiente link: http://www.juntadeandalucia.es/averroes/centros-tic/41009470/helvia/aula/archivos/repositorio/0/193/html/recursos/la/U14/pages/recursos/143304_P197/es_carcasa.html
Actividad #2:Realiza las páginas 143 y 247 del libro exploradores.
Miércoles 16 de Septiembre de 2020
Cilindros, conos y esferas
Ingresa al siguiente link y únete a la videollamada:
https://meet.google.com/noc-hpgs-rom?hs=122&authuser=2
Resuelve las siguientes preguntas:
Tarea:
Lunes 21 de Septiembre de 2020
 kms
kms
https://meet.google.com/noc-hpgs-rom?hs=122&authuser=2
Resuelve las siguientes preguntas:
Tarea:
Lunes 21 de Septiembre de 2020
Unidades de volumen
Ingresa al siguiente link y únete a la videollamada:
https://meet.google.com/fdx-dxut-cpm?hs=122&authuser=2
https://meet.google.com/fdx-dxut-cpm?hs=122&authuser=2
El volumen corresponde
a la medida del espacio que ocupa un cuerpo. La unidad de medida para medir
volumen es el metro cubico (m3), sin embargo generalmente se utiliza el Litro
(L). El metro cubico corresponde a medir las dimensiones de un cubo que mide 1
m de largo, 1 m de ancho y 1 m de alto.
La unidad principal
de volumen es el metro cúbico. Otras unidades de
volúmenes son:
kilómetro cúbico
|
km3
|
1 000 000 000 m3
|
hectómetro cúbico
|
hm3
|
1 000 000m3
|
decámetro cúbico
|
dam3
|
1 000 m3
|
metro cúbico
|
m3
|
1 m3
|
decímetro cúbico
|
dm3
|
0.001 m3
|
centímetro cúbico
|
cm3
|
0.000001 m3
|
milímetro cúbico
|
mm3
|
0.000000001 m3
|
Observamos
que desde los submúltiplos, en la parte inferior, hasta los múltiplos, en la
parte superior, cada unidad vale 1000 más que la anterior. Por lo
tanto, el problema de convertir unas unidades en otras se reduce a multiplicar
o dividir por la unidad seguida de tantos tríos de ceros como lugares haya
entre ellas.
Conversión de
unidades
Pasar 1.36 Hm3 a
m3: Tenemos que multiplicar, porque el Hm3 es
mayor que el m3 ; por la unidad seguida de seis ceros,
ya que hay dos lugares entre ambos. 1.36
· 1 000 000 = 1 360 000 m3
Pasar 15 000 mm3 a cm3: Tenemos que dividir,
porque el mm3 es menor que el cm3 , por
la unidad seguida de tres ceros, ya que hay un lugar entre ambos. 15 000 : 1000 = 15
cm3
Actividad #1: Realiza las siguientes conversiones:
- 5 m3 =…………..…..dm3;
- 7 dm3 = ………... mm3;
- 7526 cm3 = …………dm3
- 560 dam3 =………… hm3;
- 15 km3 =…………hm3;
- 86 m3 =…………….. hm3
- 0,56 m3 =…………… cm3;
- 23,56 dm3 = ……. m3;
- 0,6 dm3 =……….……cm3
Miércoles 23 de Septiembre de 2020
Unidades de volumen
Ingresa al siguiente link y únete a la videollamada:
https://meet.google.com/mdc-iyct-okj?hs=122&authuser=2
Actividad #1: Realiza las páginas 145 y 248 de exploradores.
https://meet.google.com/mdc-iyct-okj?hs=122&authuser=2
Actividad #1: Realiza las páginas 145 y 248 de exploradores.
Lunes 28 de Septiembre de 2020
Volumen de un prisma
Ingresa al siguiente link y únete a la videollamada:
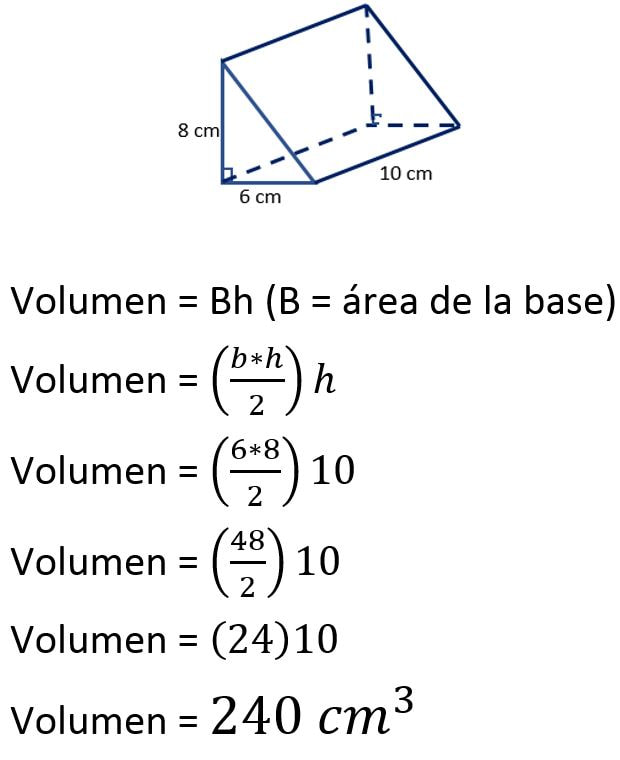
Para calcular el volumen de un prisma, multiplicamos el área de la base por la medida de la altura.
Actividad #1: Encuentra el volumen de los siguientes prismas:
Miércoles 30 de Septiembre de 2020
Volumen de un prisma
Ingresa al siguiente link y únete a la videollamada:
Actividad #1: Realiza los siguientes ejercicios:
Miércoles 14 de octubre de 2020
Volumen de un prisma
Ingresa al siguiente link y únete a la videollamada:
Actividad #1: Realiza las páginas 147 y 249 de exploradores.
Lunes 19 de octubre de 2020
Volumen de un prisma
Ingresa al siguiente link y únete a la videollamada:
Actividad #1: Realiza las páginas 152, 153 y 154 de exploradores.
Miércoles 21 de octubre de 2020
Razones y proporciones
Ingresa al siguiente link y únete a la videollamada:
Actividad #1: Realiza las páginas 252, 253 y 167 de exploradores.
Tarea: Realiza la página 254 de exploradores.
Lunes 26 de octubre de 2020
Regla de tres simple directa
Ingresa al siguiente link y únete a la videollamada:
La regla de tres simple y directa consiste en una relación de cantidades con proporcionalidad directa, que se da cuando dadas dos cantidades correspondientes a magnitudes directamente proporcionales (tienen relación), se debe calcular la cantidad de una de estas magnitudes correspondiente a una cantidad dada de la otra magnitud.
Es decir, cuando una magnitud aumenta la otra también lo hace, y si la magnitud disminuye la otra de igual forma.
Ejemplos de la regla de tres simple y directa
- Un automóvil recorre
 km en
km en  horas. ¿Cuántos kilómetros habrá recorrido en
horas. ¿Cuántos kilómetros habrá recorrido en  hora.
hora.
Solución:
 kms
kms¡Hazlo tu!
- Ana compra
 kg de papás, si
kg de papás, si  kg cuestan $2.000, ¿cuánto pagará Ana?
kg cuestan $2.000, ¿cuánto pagará Ana? - Juan Camina 12 km en tres horas ¿cuántos km recorre si camina durante 8 horas?
Tarea: Realiza los siguientes ejercicios:
1.
2.
Miércoles 28 de octubre de 2020
Regla de tres simple directa
Ingresa al siguiente link y únete a la videollamada:
ACTIVIDAD #1: Realiza las páginas 255 y 171 de exploradores.
Tarea: Realiza la página 256 de exploradores.
Martes 03 de Noviembre de 2020
Porcentajes, fracciones y decimales
Ingresa al siguiente link y únete a la videollamada:
Actividad #1: Realiza las páginas 171 y 256 de exploradores.
Miércoles 04 de Noviembre de 2020
Porcentajes, fracciones y decimales
Ingresa al siguiente link y únete a la videollamada:
Actividad #1: Realiza las páginas 175 y 177 de exploradores.
TAREA: Realiza las páginas 258 y 259 de exploradores.
Lunes 09 de Noviembre de 2020
Taller de repaso
Ingresa al siguiente link y únete a la videollamada:
Resuelve el siguiente taller:
Martes 10 de Noviembre de 2020
Figuras semejantes
Ingresa al siguiente link y únete a la videollamada:
Actividad #1: Realiza las páginas 180 y 181 de exploradores.
Miércoles 11 de Noviembre de 2020
Figuras semejantes
Ingresa al siguiente link y únete a la videollamada:
Actividad #1: Realiza las páginas 183 y 261 de exploradores.





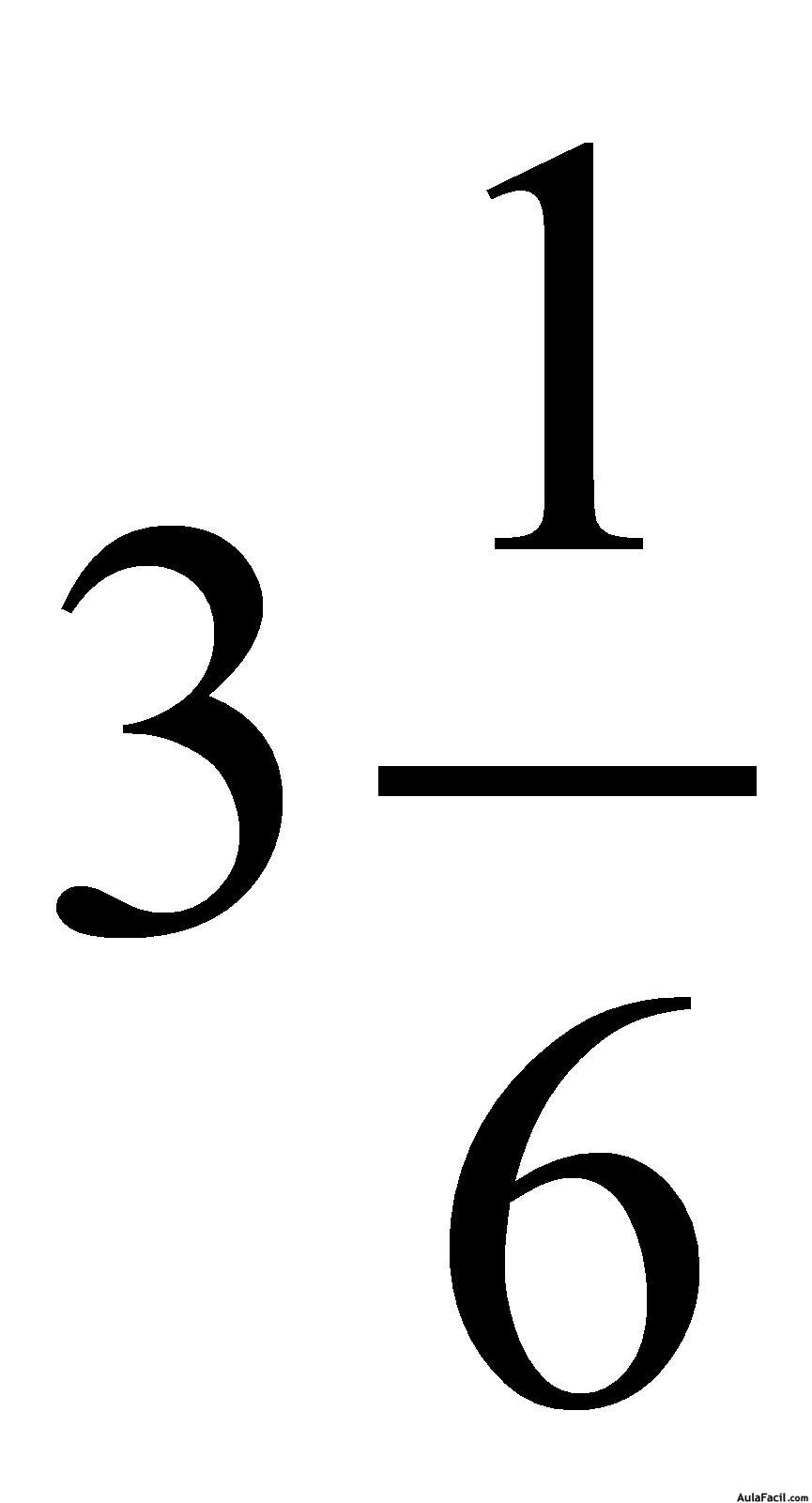








.jpg)















































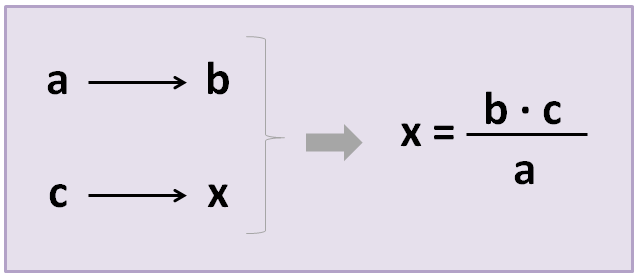




mea pare se
ResponderEliminarProfesora que hago es que se descargó el celular
ResponderEliminarProfe:-(
ResponderEliminarY los otros celulares están ocupados
ResponderEliminarY es hoy escribiendo desde mi tablet uno es compatible con meet
ResponderEliminarProfe que hacen
ResponderEliminarSe me descargo el celular
ResponderEliminar